Nielit Scientist-B IT 22-07-2017
Question 1 |
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is
E | |
2E | |
V | |
2V |
Question 1 Explanation:
Theorem (Sum of Degrees of Vertices Theorem):
Suppose a graph has n vertices with degrees d 1 , d 2 , d 3 , ..., d n.
Add together all degrees to get a new number
d 1 + d 2 + d 3 + . .. + d n = D v . Then D v = 2 e .
In words, for any graph the sum of the degrees of the vertices equals twice the number of edges.
Suppose a graph has n vertices with degrees d 1 , d 2 , d 3 , ..., d n.
Add together all degrees to get a new number
d 1 + d 2 + d 3 + . .. + d n = D v . Then D v = 2 e .
In words, for any graph the sum of the degrees of the vertices equals twice the number of edges.
Question 2 |
Which of the following is an advantage of adjacency list representation over adjacency matrix representation of a graph?
In adjacency list representation, space is saved for sparse graphs. | |
Deleting a vertex in adjacency list representation is easier than adjacency matrix representation | |
Adding a vertex in adjacency list representation is easier than adjacency matrix representation. | |
All of the option |
Question 2 Explanation:
Adjacency Matrix
● Uses O(n 2 ) memory
● It fast to lookup and check for presence or absence of a specific edge between any two nodes O(1)
● It slow to iterate over all edges
● It slow to add/delete a node is a complex operation O(n 2 )
Adjacency List
● Use memory pending on the number of edges (not number of nodes), Which might save a lot of memory if the adjacency matrix is a sparse
● Finding the presence or absence specific edge between any two nodes Is slightly slower than with the matrix O(k) where k number of neighbors nodes
● It is fast to iterate over all edges,because you can access any node neighbors directly
● It is fast to add/delete a node is easier than the matrix representation
● Uses O(n 2 ) memory
● It fast to lookup and check for presence or absence of a specific edge between any two nodes O(1)
● It slow to iterate over all edges
● It slow to add/delete a node is a complex operation O(n 2 )
Adjacency List
● Use memory pending on the number of edges (not number of nodes), Which might save a lot of memory if the adjacency matrix is a sparse
● Finding the presence or absence specific edge between any two nodes Is slightly slower than with the matrix O(k) where k number of neighbors nodes
● It is fast to iterate over all edges,because you can access any node neighbors directly
● It is fast to add/delete a node is easier than the matrix representation
Question 3 |
A path in graph G, which contains every vertex of G and only Once?
Euler circuit | |
Hamiltonian path | |
Euler Path | |
Hamiltonian Circuit |
Question 3 Explanation:
● Hamiltonian path, also called a Hamilton path, is a graph path between two vertices of a graph that visits each vertex exactly once. If a Hamiltonian path exists whose endpoints are adjacent, then the resulting graph cycle is called a Hamiltonian cycle (or Hamiltonian cycle)
● An Euler path is a path that uses every edge of a graph exactly once. An Euler circuit is a circuit that uses every edge of a graph exactly once.
● An Euler path starts and ends at different vertices.
● An Euler circuit starts and ends at the same vertex.
● An Euler path is a path that uses every edge of a graph exactly once. An Euler circuit is a circuit that uses every edge of a graph exactly once.
● An Euler path starts and ends at different vertices.
● An Euler circuit starts and ends at the same vertex.
Question 4 |
what are the appropriate data structures for graph traversal using Breadth First Search(BFS) and Depth First Search(DFS) algorithms?
Stack for BFS and Queue for DFS | |
Queue for BFS and Stack for DFS | |
Stack for BFS and Stack for DFS | |
Queue for BFS and Queue for DFS |
Question 4 Explanation:
● Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
● Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key'), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
● Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key'), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
Question 5 |
In a given following graph among the following sequences:
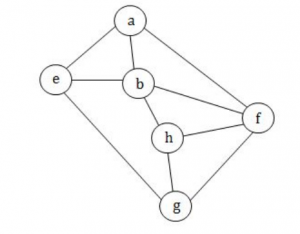
i)abeghf
ii)abfehg
iii)abfhge
iv)afghbe
Which are depth first traversals of the above graph?

i)abeghf
ii)abfehg
iii)abfhge
iv)afghbe
Which are depth first traversals of the above graph?
I,II and IV only | |
I and IV only | |
II,III and IV only | |
I,III and IV only |
Question 5 Explanation:
The basic idea of DFS is
● Pick a starting node and push all its adjacent nodes into a stack.
● Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
● Repeat this process until the stack is empty. However, ensure that the nodes that are visited are marked.
● This will prevent you from visiting the same node more than once. If you do not mark the nodes that are visited and you visit the same node more than once, you may end up in an infinite loop.
● Pick a starting node and push all its adjacent nodes into a stack.
● Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
● Repeat this process until the stack is empty. However, ensure that the nodes that are visited are marked.
● This will prevent you from visiting the same node more than once. If you do not mark the nodes that are visited and you visit the same node more than once, you may end up in an infinite loop.
Question 6 |
Considering the following graph, which one of the following set of edged represents all the bridges of the given graph?
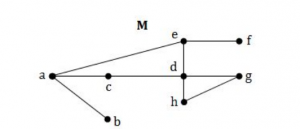

(a,b)(e,f) | |
(a,b),(a,c) | |
(c,d)(d,h) | |
(a,b) |
Question 6 Explanation:
● A bridge ,cut-edge, or cut arc is an edge of a graph whose deletion increases its number of connected components.
● Equivalently, an edge is a bridge if and only if it is not contained in any cycle.
● The removal of edges (a,b) and (e,f) makes graph disconnected.
● Equivalently, an edge is a bridge if and only if it is not contained in any cycle.
● The removal of edges (a,b) and (e,f) makes graph disconnected.
Question 7 |
Which of the following statements is/are TRUE?
S1: The existence of an Euler circuit implies that an euler path exists.
S2: The existence of an Euler path implies that an Euler circuit exists.
S1: The existence of an Euler circuit implies that an euler path exists.
S2: The existence of an Euler path implies that an Euler circuit exists.
S1 is true | |
S2 is true | |
S1 and S2 both are true | |
S1 and S2 both are false |
Question 7 Explanation:
An Euler circuit in a graph G is a simple circuit containing every edge of G exactly once
An Euler path in G is a simple path containing every edge of G exactly once.
An Euler path starts and ends at different vertices.
An Euler circuit starts and ends at the same vertex.
An Euler path in G is a simple path containing every edge of G exactly once.
An Euler path starts and ends at different vertices.
An Euler circuit starts and ends at the same vertex.
Question 8 |
A connected planar graph divides the plane into a number of regions. If the graph has eight vertices and these are linked by 13 edges, then the number of regions is:
5 | |
6 | |
7 | |
8 |
Question 8 Explanation:
Use Euler's formula ,V−E+R=2
Where V is the number of vertices, E is the number of edges, and R is the number of regions.
R=2-V+E=2-8+13=7
Where V is the number of vertices, E is the number of edges, and R is the number of regions.
R=2-V+E=2-8+13=7
Question 9 |
Power set of empty set has exactly__subset
One | |
Two | |
Zero | |
Three |
Question 9 Explanation:
● The collection of all subsets of a set A is called the power set of A.
● The empty set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero
● Common notations for the empty set include "{}", " ", and "∅".
● The empty set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero
● Common notations for the empty set include "{}", " ", and "∅".
Question 10 |
What is the cartesian product of A={1,2} and B={a,b}?
{(1,a),(1,b),(2,a),(b,b)} | |
{(1,1),(2,2),(a,a),(b,b)} | |
{(1,a),(2,a),(1,b),(2,b)} | |
{(1,1),(a,a),(2,a),(1,b)} |
Question 10 Explanation:
● A Cartesian product is a mathematical operation that returns a set (or product set or simply product) from multiple sets. That is, for sets A and B, the Cartesian product A × B is the set of all ordered pairs (a, b) where a ∈ A and b ∈ B.
● In the question, Set A consists of two elements and Set B consists of two elements. So the total ordered pairs are four.
● Each ordered pair consists of one element from Set-A and another element from Set-B.
● In the question, Set A consists of two elements and Set B consists of two elements. So the total ordered pairs are four.
● Each ordered pair consists of one element from Set-A and another element from Set-B.
Question 11 |
What is the cardinality of the power set of the set {0,1,2}?
8 | |
6 | |
7 | |
9 |
Question 11 Explanation:
The cardinality of a set is defined as the total number of distinct items in that set and power set is defined as the set of all subsets of a set.
Power set consists of {}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}
So power set consists of all unique items then cardinality is 8
Power set consists of {}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}
So power set consists of all unique items then cardinality is 8
Question 12 |
Let G be a simple connected planar graph with 13 vertices and 19 edges. then the number of faces in the planar embedding of the graph is
6 | |
8 | |
9 | |
13 |
Question 12 Explanation:
● Use Euler's formula ,V−E+R=2
● Where V is the number of vertices, E is the number of edges, and R is the number of regions.
● R=2-V+E=2-13+19=8
● We can also term region as face
● Where V is the number of vertices, E is the number of edges, and R is the number of regions.
● R=2-V+E=2-13+19=8
● We can also term region as face
Question 13 |
Which of the following statements is false?
(P⋀Q)V(~P⋀Q)V(P⋀~Q) is equal to ~Q⋀~P | |
(P⋀Q)V(~P⋀Q)V(P⋀~Q) is equal to QVP | |
(P⋀Q)V(~P⋀Q)V(P⋀~Q) is equal to QV(P⋀~q) | |
(P⋀Q)V(~P⋀Q)V(P⋀~Q) is equal to PV(Q⋀~p) |
Question 13 Explanation:
One simple method is, by using truth table we can find the statement is true or not.
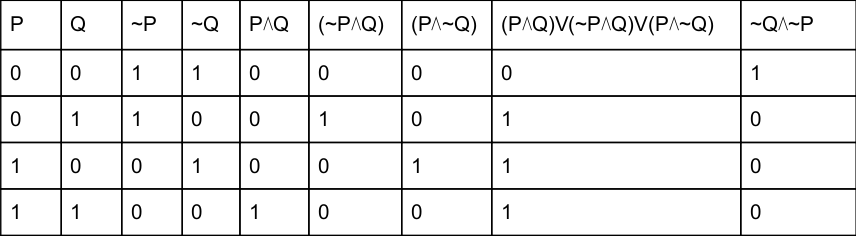
The last two columns of the above table are different. So option A is false.

The last two columns of the above table are different. So option A is false.
Question 14 |
There are four bus lines between A and B; And three bus lines between B and C The number of way a person roundtrip by bus from A to C by way of B will be
12 | |
7 | |
144 | |
264 |
Question 14 Explanation:
The number of bus lines between a and b =4
The number of bus lines between b and c =3
The number of possible combinations between a and c going through b are 4 * 3 = 12.
if you're talking about round trip, he has 12 possible ways to get there and 12 possible ways to get back, so the total possible ways is 12 * 12 = 144.
The number of bus lines between b and c =3
The number of possible combinations between a and c going through b are 4 * 3 = 12.
if you're talking about round trip, he has 12 possible ways to get there and 12 possible ways to get back, so the total possible ways is 12 * 12 = 144.
Question 15 |
The number of diagonals that can be drawn by joining the vertices of an octagon is
28 | |
48 | |
20 | |
None of the option |
Question 15 Explanation:
Octagon consists of the 8 vertices and we can draw 5 diagonals
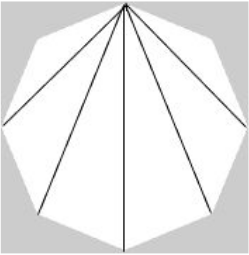
So, we can construct 5*8 = 40 diagonals.
But we have constructed each diagonal twice, once from each of its ends. Thus there are 20 diagonals in a regular octagon.

So, we can construct 5*8 = 40 diagonals.
But we have constructed each diagonal twice, once from each of its ends. Thus there are 20 diagonals in a regular octagon.
There are 15 questions to complete.
